Project Rupert Klein and Michael Oevermann

Summary:
Many important industrial chemical processes and naturally occurring phenomena can be described by the equations for variable density zero Mach number two-phase flow with heat and mass transfer across an interface separating the two fluids. Some of the main challenges in modeling and simulating such flows are discontinuous solutions (pressure, density, concentration), large ratios of physical variables (viscosity, diffusivity, conductivity) across an interface, and the solution of transport equations on moving surfaces.
This research project focus on the proper design of a locally second order accurate finite volume method for zero Mach number two-phase flow with soluble surfactants and mass transfer across an immiscible interface. Based on our previous work we specifically address the following issues:

1. design of a conservative sharp interface finite volume projection method on Cartesian grids with explicit representation of discontinuities,
2. development of a conservative finite volume discretisation of the surface surfactant equation,and
3. implementation of an asymptotics based efficient solution strategy for the variable coefficient Poisson equation for interface problems with arbitrarily large ratio of the coefficients.

With our research project we contribute directly to the goal of the DFG Priority Program SPP 1506 to develop "numerical methods for the simulation of multiphase flow problems which resolve the local processes at the interface".

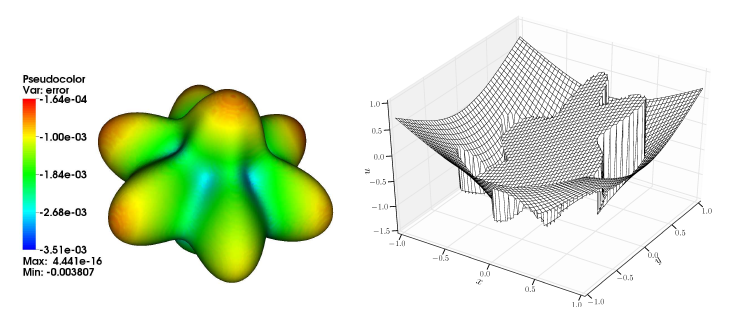
Figure 1: Sharp interface solution of the Poisson equation with a complex embedded interface.
Left: solution error on the interface, right: discontinuous solution at a cut through the interface.