Project Helmut Abels

Abstract
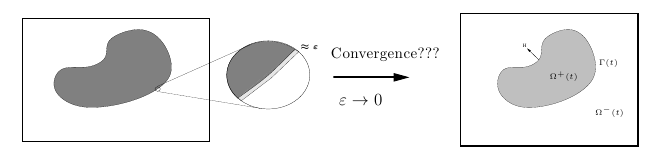
We seek a rigorous understanding of sharp interface limits of so-called diffuse interface models for the flow of two viscous fluids like oil and water. In diffuse interface models a partial mixing of the macroscopically immiscible fluids on a small length scale ε > 0 and diffusion of the mass particles are taken into account. These models are capable of describing such two-phase flows beyond the occurrence of topological singularities of the interface due to collision or droplet formation. Both for theoretical and numerical purposes a deeper understanding of the limit ε → 0 in dependence of the scaling of the mobility mε is of interest. Here the mobility is the inverse of the Peclet number and controls the strength of the diffusion. In particular, we want to understand the influence of the scaling of the mobility coefficient mε as ε → 0 on the limit system and on the convergence rates rigorously. This way we want to clarify numerical observations and formal derivations in the literature and obtain new insights.